Heat pumps have the mythic characteristic of providing a nominal yield of more than 100%, with values in the range of 200-400%.  This is due to the few energy necessary, to make the heat transfer fluid transport the captured heat, in comparison to the amount of heat offtaken from the atmosphere or the soil.

But, is the nominal yield applicable over a whole year ? or rather, since the amount of captured heat diminishes when the outside (atmospheric) temperature also does, requiring a higher average flow rate to deliver (transfer) the same amount of energy, while the necessary amount of energy to heat the dwelling increases (due to the lower outside temperature), can we estimate the influence of the (outside) temperature on this yield and calculate its yearly (usage) weighted average ?

Let us examine each element and then gather them all to draw conclusions.

A heat pump captures heat by evaporation of a low boiling point fluid (let us say around -10°C to ‑20°C), the heat coming from the atmospheric air (for the air pump), being at (outside) ambient temperature, or from the soil (for the water-glycol pumps).  Since the soil heat pump type has nearly disappeared, due to its high installation costs, we will focus on the air heat pump.

So, for this type, the captured heat is proportional to the difference of temperature between the atmospheric air and the boiling point of the fluid.  Thus, when the (outside) air temperature increases, the capturable heat also does and, conversely, when the air temperature decreases, the capturable heat also decreases:

Qp = K1 . (Te – Tb)

where: Qp is the captured (pumpable) heat (during a definite time, e.g. by cycle), Te being the outside temperature and, Tb the boiling temperature of the heat transfer fluid.  The multiplication factor (K1) is just the (global) heat transfer coefficient, which depends on the physical and technical characteristics of the installation.

 

Now, once the heat has been captured, it must still be transported into the dwelling (and there, exchanged with the heating system).  This transport is achieved using a pump (rather a turbocharger since the heat is vehicled by the vapour of the evaporated fluid).  The energy consumed by the pump (during a definite time) is proportional to the necessary heat flow rate that must be delivered by the fluid (heat by cycle multiplied by the duration of working time and divided by the sum of the working + idle time, e.g. by hour).

To maintain the same energy transfer rate (= heating power for the dwelling heating system) when the amount of captured heat (by cycle) decreases, the pump must run the circulation more frequently, thus enlarge the working time and reduce the idle (e.g. by hour or, globally, by day), thus increase the flow rate of the heat transfer:

P = K2 . qf

where: P is the energy consumed by the pump (during a definite time, e.g. by cycle), qf the flow rate of the heat transfer.  K2 is related to the pressure drop factor of the heat transfer circuit (but not by the dwelling heating system) and the physical characteristics of the fluid.

 

The necessary heat transfer rate increases when the dwelling requires more heat, it is indeed proportional to the (total) heat loss of the dwelling, which is, in turn, proportional to the difference between the inside and outside temperature:

Qh = K3 . (Ti – Te)

qf = K4 . Qh / Qp

where: Qh is the necessary heat (during a definite time, e.g. by cycle) to counter the heat losses of the dwelling, Ti being the (desired/regulated) inside temperature of the dwelling.  K3 is the heat loss coefficient of the dwelling and K4 is the heat transfer ratio from the pumped heat to the heating (system) of the dwelling.

 

Considering that the transfer of the transported heat (by the heat pump circuit) into the dwelling (through its heating system, very often a floor heating system) occurs at constant yield (independent of the flow rate of the heat transfer fluid), we can calculate the yield of the installation.

The yield, for any engine, is the ratio of the useful energy (here, Qp), divided by the onerous energy (here, P), applied to the heat pump, we have:

r = Qp / P = Qp / K2 . qf = Qp / K2 . (K4 . Qh / Qp) = K5 . (Qp)² / Qh
and finally:                         r = K . (Te – Tb)² / (Ti – Te)

where: K5 groups the multiplication/division/power of the underlying K2 and K4 and, K do the same for K5, K1 and K3.  There are all no more than factors.

 

The yield is thus proportional to the 2^nd power of the temperature span between the atmospheric temperature and the boiling point of the fluid, divided by the temperature span between the dwelling inside temperature and the outside temperature.

Neither easy to interpret nor to visualize, so let us take an example.  Suppose the nominal (design) values are:

Tb = -20°C (boiling point of heat transfer fluid), Te = 10°C (yearly atmospheric temperature average in Belgium), Ti = 20°C (desired dwelling temperature) and r = 300% (300/100 = 3), we have:

3 = K (10 – (-20))² / (20 – 10)           thus       K = 0,0333

The value of K, in itself, is not so interesting here, it is just necessary to calculate the value of r in other circumstances.  Let us see, for this heat pump, what becomes the yield when the outside temperature dives to respectively 5°C, 0°C, -5°C and -10°C:

for Te =    5°C we have r = 1,39 (thus 139%),

for Te =    0°C we have r = 0,667 (thus 67%),

for Te =   -5°C we have r = 0,300 (thus 30%),

for Te = -10°C we have r = 0,111 (thus 11%),

remark: with a Tb of -10°C, the figures would be far worse (already no more than 113% at 5°C and 37,5% at 0°C).

It is noticeable that the yield is very much lower (67% at 0°C and 30% at -5°C) than the nominal one (300%), when the outside temperature dives below the design temperature.

Of course when the outside temperature is as low as the boiling temperature of the heat transfer fluid (in this case -20°C), no heat can be captured and the heat pump stops working (rather: has no idle time anymore while delivering no heat transfer, and thus falls down into security mode and stops).

Awful, yes, but the whole system is provided with an insulated water vessel (where the heat is transferred to the dwelling heating system), of around 300l, heated by the heat pump, but supported by an electrical (heating) resistance, installed for several purposes among which the heating of the (vessel) water when the heat pump is not working, a kind of fall back (but with a yield that is a little bit below 100%).  One can notice that it would be suitable to switch from the heat pump to the resistance when the yield of the heat pump becomes lower than 100%, in those circumstances, the resistance has indeed a higher yield than the heat pump.

Now, of course the heat pump will work more in the winter than in the spring and nearly not in the summer (in this season, it works only for the preparation of hot water, e.g. for showers).  So, the actual operating temperature is rather between 15°C (fall, spring) till downto -10°C (seldom lower).

Due to the strong non-linear character of the expression of the yield, we have to use daily temperatures to achieve the daily calculation of the useful energy as well as of the onerous one, then sum up them both (separately) over a whole year, and finally divide the first sum by the latter one to get the average (weighted) yield.

The problem is that no year is standard, some days, weeks and months are warmer in one year than in other, while we want to have a standard year value for the yield, or at least approximate it.

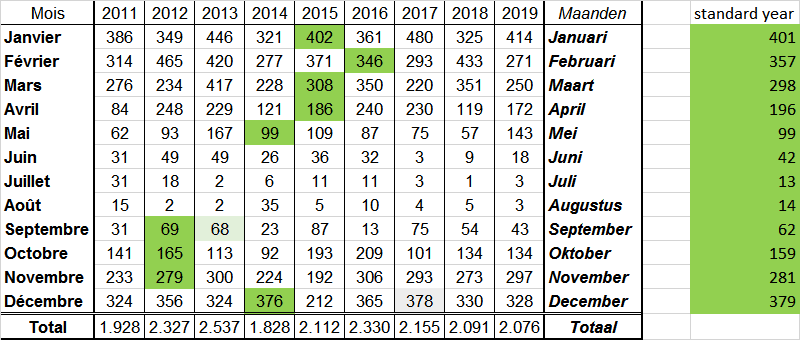
Fortunately, the heating needs are expressed in degree-days and there exist standard (monthly) values for them (see the rightmost column, in the table below) and so, for each month, it is possible to find a year in which the heating need was the nearest to the standard year one:

With this information, it is possible to retrieve the average daily temperature for each day (from specialized sites) and calculate the useful energy (Qh, setting the K1 factor on 1).  Then, to free us up from the K1 factor, we will divide Qh by the sum of Qh over the whole year, getting a normalized Qh (Qh norm), expressed in % of the total necessary yearly heating energy.

The yield is than calculated for each day (on the basis of the average daily temperature), so that the onerous energy can be calculated too, by dividing the daily normalized Qh by the daily yield.

One could argue that using daily average for the temperature, instead of hourly values, is not correct, due to the strong non-linear character of the yield.  This is a theoretical correct objection, but the temperature inside the home, combined with the fact that the water vessel acts as a kind of buffer, will make the things matching the daily average (better than finer granularity like hourly values).  Further, if a finer granularity would give more accurate results, they would be to the detriment of calculated yield (as it is already the case when refining from a yearly or monthly averages to daily averages).

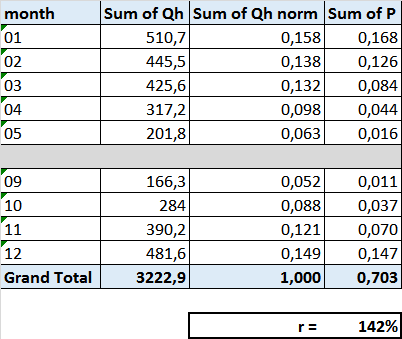
The result of the calculations are shown in the table below:

The summer months (June-August) have not been used in the calculation, in these months there is normally no heating necessary (except for hot water preparation, but this is not part of the analysis and represents very few energy in comparison).  The normalized Qh shows that January tells for nearly 16% (0,158) of the yearly heating energy, while September does not reach 6% (0,052) of it.

We also see that P (the onerous energy) is lower than the normalized Qh in nearly all months (except January).  But the yield (division of Qh norm by P) remains always far under 2, except for the months of April to October, thus when the heating need is low.  One could say, ironically, that the heat pump figures out a high yield only when it does not work (much).

The total of the onerous energy necessary to pump a yearly normalized Qh of 1 is of 0,703 (in the same unit).  This means that we need, as heating needs weighted average, 0,703 kWh (or MJ or BTU is you want) of onerous energy to retrieve 1 kWh (or MJ or BTU is you want) of heat, giving a global yield of 142%.  It is less than half of the nominal value but still quite higher than 100%, so it seems good.  But is it really so ?

The energy used by the heat pump is electricity, coming from the grid.  This electricity must be generated by powerstations of different kinds (at very high voltage, typically 150kV to 380 kV), having a global mix average yield of 45% (being the ratio of the generated electricity divided by the related fossil energy burned for this purpose), and transmitted through the grid downto (the low voltage level of) the dwelling, incurring an energy loss of roughly 10%.

So the electricity used has finally a yield of 40,5% (45% × (100 – 10)%).  The global energetic yield of the heat pump is thus of: 142% × 40,5% = 57,5%.

In turn, a common gas boiler has got an efficiency of 90% (higher for a condensing one), from which the energy used for its transport and distribution must be subtracted.  Using the same 10% as for electricity, which is more than excessive since gas transport does not require much energy, we have a yield laying above 80%.

Of course, one could argue that the electricity can be produced renewably.  That is right, but not using solar panels (in Belgium) since they produce mainly in the summer while the heating occurs mainly in the winter (solar panels don’t produce in the winter, or very few, their production becomes substantial only from March-April, till September-October and then only during daylight time).  Wind energy could be a source, if it would reliably feed the pump when the meteorological circumstance will require the heat pump to run (which is not necessarily when the wind blows sufficiently).

Further, methane can also be produced renewably (renewable electricity -> hydrogen -> methane with capture of CO2) and easily stored when abounding (i.e. in the summer) for later use (i.e. in the winter).

Since the dwellings where heat pumps are installed show generally low heat losses, the energy consumption for heating is limited to roughly (something around) 10 MWh/y, the related consumption of electricity is thus of 10/142% = 7 MWh/y, for a cost (in Belgium ) of (depending on the DGO area and the user supply contract) 2.100 €/y, while the gas consumption should be of 10/90% = 11 MWh/y for a cost (in Belgium ) of (depending on the DGO area and the user supply contract) 440 €/y, showing an extra cost of 1.660 €/y for the heat pump, without taking into account its higher installation cost.

This higher installation and consumption costs are perhaps compensated (till a certain level) by subsidies (or tax reduction, which is equivalent to a subsidy), but these are paid by the other citizens (through the tax on their income and others).

Environmentally, the global primary energy consumption for the heat pump is of 10/57,5% = 17,4 MWh/y, while for the gas boiler it would be of 10/80% = 12,5 MWh/y, showing a footprint which is roughly 40% higher for the heat pump.

The question is thus, ¿ why are heat pumps promoted ?  Or rather ¿ which party has the highest interest in generalizing it ? As detective Hercule Poirot used to say, look for whom is benefiting from it … it is surely not the customer … nor the citizen and, … as additional tip, I can ensure you it is definitively not the supplier.